回溯算法学习笔记
什么是回溯算法?
回溯算法通过穷举来解决问题,暴力搜索,遇到正确的解则记录,在某个状态无法前进或无法满足条件时,回退到上一步状态,再尝试其他的选择。回溯算法通常采用深度优先搜索进行遍历。
[!NOTE]
回溯算法适合处理无法预测哪些是有效的解,必须对所有可能的解进行遍历的情况。因此并不适合处理大规模或复杂问题。
时间复杂度:由于需要遍历所有可能的解,可能会达到
O(n^k)。空间复杂度:需要在遍历过程中记录当前状态,随着深度的增大,对空间的需求也会增大。
回溯算法常见的问题
全排列
无重复元素全排列
详情请见LeetCode-46 全排列。
| 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 |
|---|
| 示例1: 输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例2: 输入:nums = [0,1] 输出:[[0,1],[1,0]] 示例3: 输入:nums = [1] 输出:[[1]] |
思路
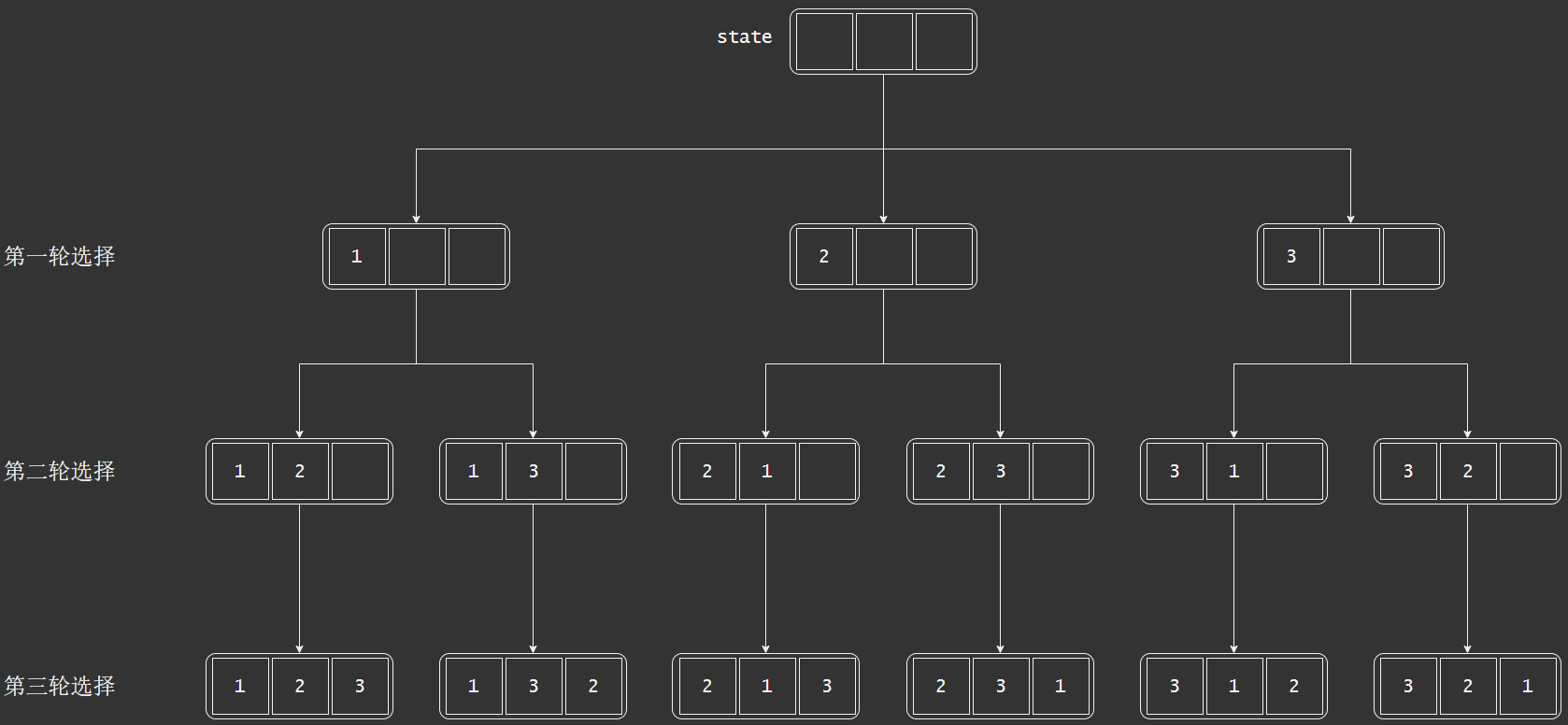
将生成结果的过程看成逐个选择。
对于示例1,可以先选择1,再选择2,最后选择3,则获得排列[1, 2, 3];然后回退到第二次选择,选择3,然后再选择2,得到[1, 3, 2]。
对于上述选择还要进行剪枝。例如第一轮选择了1之后,第二轮不能再重复选择1。我们可以通过
boolean数组selected记录当前元素是否被选择。代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
backtrack(new ArrayList<>(), nums, new boolean[nums.length], result);
return result;
}
private void backtrack(List<Integer> state, int[] nums, boolean[] selected, List<List<Integer>> result) {
// 已选择所有元素,添加到结果集中
if (state.size() == nums.length) {
result.add(new ArrayList<Integer>(state));
return;
}
// 遍历未选择的元素
for (int i = 0; i < nums.length; i++) {
// 剪枝,跳过已选择的元素
if(!selected[i]){
selected[i] = true;
state.add(nums[i]);
// 下一轮选择
backtrack(state, nums, selected, result);
// 回退
state.remove(state.size() - 1);
selected[i] = false;
}
}
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
fun permute(nums: IntArray): List<List<Int>> {
val result = mutableListOf<List<Int>>()
backtrack(mutableListOf(), nums, BooleanArray(nums.size), result)
return result
}
private fun backtrack(state: MutableList<Int>, nums: IntArray,selected: BooleanArray, result: MutableList<List<Int>>){
// 已选择所有元素,添加到结果集中
if(state.size == nums.size){
result.add(state.toList())
return
}
// 遍历未选择的元素
for(i in nums.indices){
// 剪枝,跳过已选择的元素
if(!selected[i]){
selected[i] = true
state.add(nums[i])
// 下一轮选择
backtrack(state, nums, selected, result)
// 回退
state.removeAt(state.lastIndex)
selected[i] = false
}
}
}
}
有重复元素全排列
详情请见LeetCode-47 全排列II。
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 |
|---|
| 示例 1: 输入:nums = [1,1,2] 输出: [[1,1,2], [1,2,1], [2,1,1]] 示例 2: 输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] |
思路
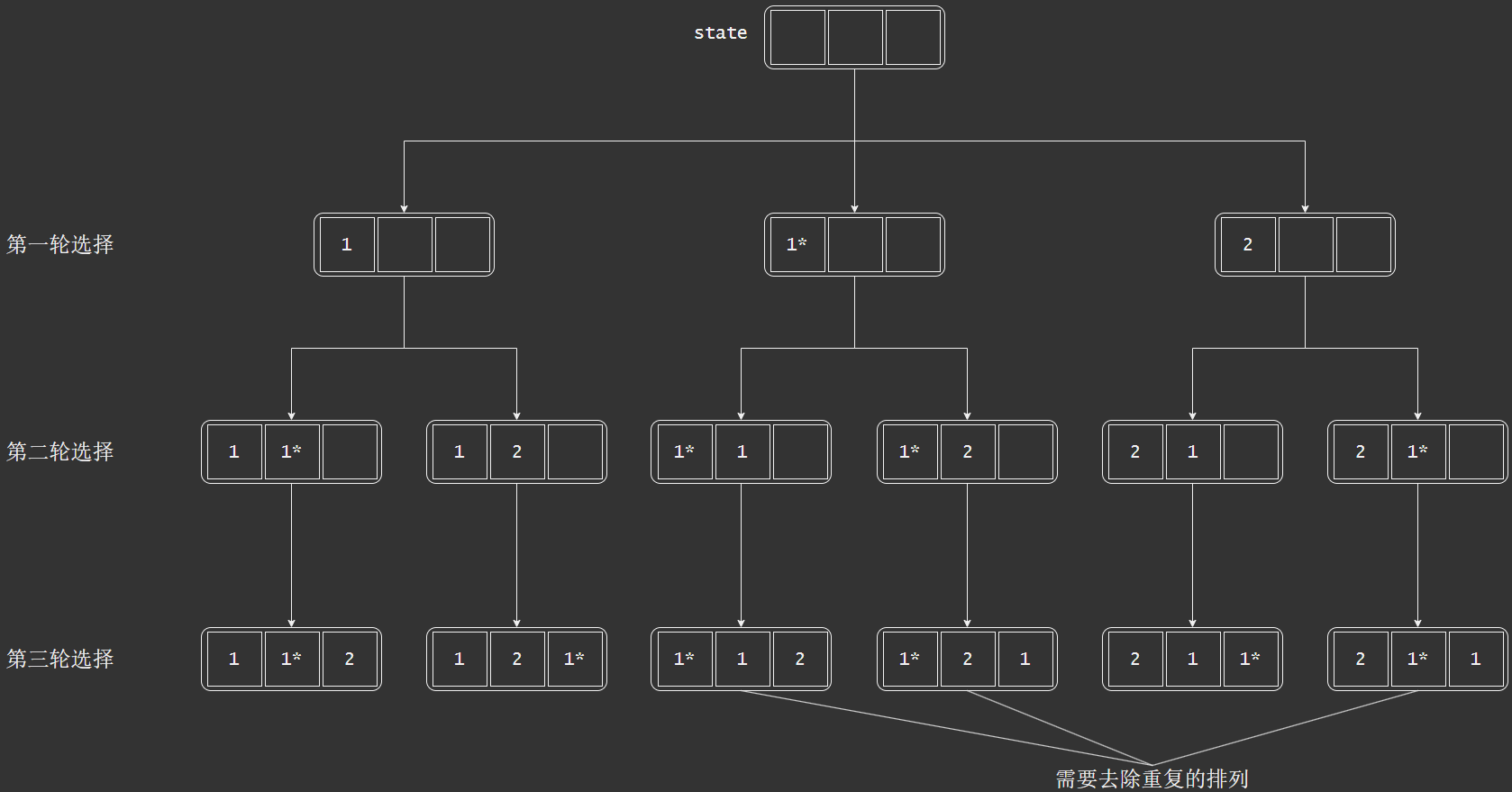
如果按照无重复全排列的选择方式,对于示例1将会有一半的重复排列。
我们需要提前识别到重复元素并剪枝,避免出现重复排列。
在第一轮选择中,选择1或1*是等价的,需要将1*剪枝。第二轮选择中也会同样产生上述情况,也需要将1*剪枝。
因此,我们需要保证多个相等的元素仅被选择一次。可以通过在每一轮选择中开启一个哈希表
duplicated,记录已经尝试过的元素,并将重复元素剪枝。代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
backtrack(new ArrayList<>(), nums, new boolean[nums.length], result);
return result;
}
private void backtrack(ArrayList<Integer> state, int[] nums, boolean[] selected, List<List<Integer>> result) {
// 当state中的元素数量等于choices时,记录解
if (state.size() == nums.length) {
result.add(new ArrayList<Integer>(state));
return;
}
// 遍历所有选择
HashSet<Integer> duplicated = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
// 剪枝,跳过已经选择过的元素和重复元素
if(!selected[i] && !duplicated.contains(nums[i])){
duplicated.add(nums[i]);
selected[i] = true;
state.add(nums[i]);
// 递归搜索
backtrack(state, nums, selected, result);
// 撤销选择
state.remove(state.size() - 1);
selected[i] = false;
}
}
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
fun permuteUnique(nums: IntArray): List<List<Int>> {
val result = mutableListOf<MutableList<Int>>()
backtrack(mutableListOf(), nums, BooleanArray(nums.size), result)
return result
}
private fun backtrack(state: MutableList<Int>, nums: IntArray, selected: BooleanArray, result: MutableList<MutableList<Int>>) {
// 当state中的元素数量等于choices时,记录解
if(state.size == nums.size){
result.add(state.toMutableList())
return
}
// 遍历所有选择
val duplicated = HashSet<Int>()
for (i in nums.indices) {
// 剪枝,跳过已经选择过的元素和重复元素
if(!selected[i] &&!duplicated.contains(nums[i])){
duplicated.add(nums[i])
selected[i] = true
state.add(nums[i])
// 递归搜索
backtrack(state, nums, selected, result)
// 撤销选择
state.removeAt(state.size - 1)
selected[i] = false
}
}
}
}
子集和
无重复元素子集和
详情请见LeetCode-39 组合总和。
| 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。 对于给定的输入,保证和为 target 的不同组合数少于 150 个。 |
|---|
| 示例 1: 输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。7 也是一个候选, 7 = 7 。仅有这两种组合。 示例 2: 输入: candidates = [3,4,5], target = 9 输出: [[3,3,3],[4,5]] 示例 3: 输入: candidates = [2], target = 1 输出: [] |
思路
我们可以参考全排列问题来解答。由于在本问题中同一元素可以被多次选取,因此无需借助
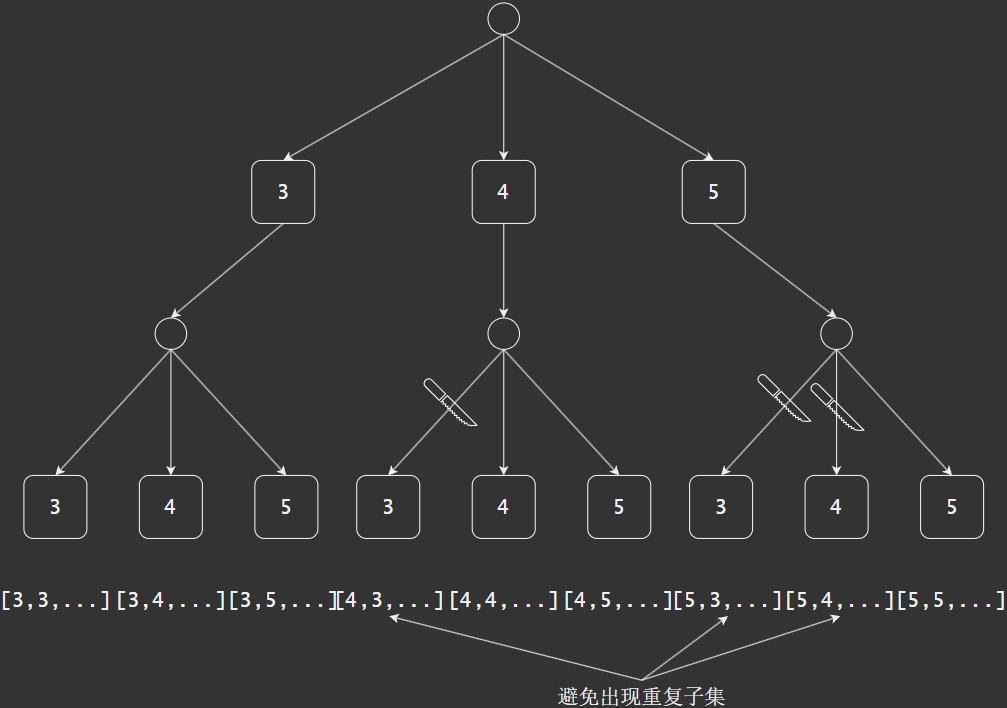
boolean数组selected来记录元素是否已经被选择。对于示例2,按照全排列解法,我们得到输出结果为[[3,3,3],[4,5],[5,4]],其中存在重复的子集[4,5]和[5,4]。因为全排列的搜索过程分选择顺序,而子集和不区分选择顺序。
我们需要在搜索过程中进行剪枝来去重。
由上图可知,当前两轮分别选择3和4得到[3,4,…]时,第二次选择4之后,下一轮选择应该跳过3,避免产生[4,3,…]和第一轮选择重复。在逐个尝试的过程中,由于是从左到右进行尝试,因此越靠近右侧的分支被剪掉的越多。通过以下三个操作来对代码进行优化:
① 通过变量
start记录遍历起始点,当做出选择candidates[i]后,下一轮选择应从i开始,从而保证子集唯一。② 在搜索前将数组
candidates排序,在子集和超过target时直接结束循环,因为后面的元素更大,其子集和一定超过target。③ 通过对
target执行减法来记录子集和,当target=0时记录解。代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(candidates);
backtrack(new ArrayList<>(), candidates, target, 0, result);
return result;
}
private void backtrack(ArrayList<Integer> state, int[] candidates,int target, int start, List<List<Integer>> result) {
// 子集和等于target,将当前子集加入结果集
if (target == 0) {
result.add(new ArrayList<>(state));
return;
}
for(int i = start; i < candidates.length; i++) {
// 子集和超过target,停止搜索
if(target - candidates[i] < 0) break;
state.add(candidates[i]);
// 递归搜索
backtrack(state, candidates, target - candidates[i], i, result);
// 回退
state.remove(state.size() - 1);
}
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
fun combinationSum(candidates: IntArray, target: Int): List<List<Int>> {
val result = mutableListOf<List<Int>>()
candidates.sort()
backtrack(mutableListOf(), candidates, target, 0, result)
return result
}
private fun backtrack(
state: MutableList<Int>,
candidates: IntArray,
target: Int,
start: Int,
result: MutableList<List<Int>>
) {
// 子集和等于target,将当前子集加入结果集
if (target == 0) {
result.add(state.toList())
return
}
for (i in start..<candidates.size) {
// 子集和超过target,停止搜索
if (target - candidates[i] < 0) break
state.add(candidates[i])
// 递归搜索
backtrack(state, candidates, target - candidates[i], i, result)
// 回退, state.lastIndex相当于state.size-1
state.removeAt(state.lastIndex)
}
}
}
有重复元素子集和
详情请见LeetCode-40 组合总和II。
| 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意:解集不能包含重复的组合。 |
|---|
| 示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8 输出: [[1,1,6],[1,2,5],[1,7],[2,6]] 示例 2: 输入: candidates = [2,5,2,1,2], target = 5 输出: [[1,2,2],[5]] |
思路
根据无重复元素子集和的解法,由于数组已经是排序的,那么相等元素必然是相邻的。因此只要判断当前元素是否和左边元素相等即可。如果相等则说明已经被选择过,因此直接跳过当前元素。本题还规定了每个数字在每个组合中只能使用一次,在上述通过
start记录起始点的情况下,当选择candidates[i]后,下一轮从i+1开始遍历,既能去除重复子集,也能避免重复选择元素。代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(candidates);
backtrack(new ArrayList<>(), candidates, target, 0, result);
return result;
}
private void backtrack(ArrayList<Integer> state, int[] candidates, int target, int start, List<List<Integer>> result) {
// 子集和等于target,将当前子集加入结果集
if (target == 0) {
result.add(new ArrayList<>(state));
return;
}
for (int i = start; i < candidates.length; i++) {
// 子集和超过target,停止搜索
if (target - candidates[i] < 0) break;
// 去重
if (i > start && candidates[i] == candidates[i - 1]) continue;
state.add(candidates[i]);
// 递归搜索
backtrack(state, candidates, target - candidates[i], i + 1, result);
// 回退
state.remove(state.size() - 1);
}
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
fun combinationSum2(candidates: IntArray, target: Int): List<List<Int>> {
val result = mutableListOf<List<Int>>()
candidates.sort()
backtrack(mutableListOf(), candidates, target, 0, result)
return result
}
private fun backtrack(
state: MutableList<Int>,
candidates: IntArray,
target: Int,
start: Int,
result: MutableList<List<Int>>
) {
// 子集和等于target,将当前子集加入结果集
if (target == 0) {
result.add(state.toList())
return
}
for (i in start..<candidates.size) {
// 子集和超过target,停止搜索
if (target - candidates[i] < 0) break
// 去重
if (i > start && candidates[i] == candidates[i - 1]) continue
state.add(candidates[i])
// 递归搜索
backtrack(state, candidates, target - candidates[i], i + 1, result)
// 回退, state.lastIndex相当于state.size-1
state.removeAt(state.lastIndex)
}
}
}
n皇后
详情请见LeetCode-51 N皇后。
| 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。 每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。 |
|---|
| 示例 1: 输入:n = 4 输出:[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]] 解释:如上图所示,4 皇后问题存在两个不同的解法。 示例 2: 输入:n = 1 输出:[[“Q”]] |
思路
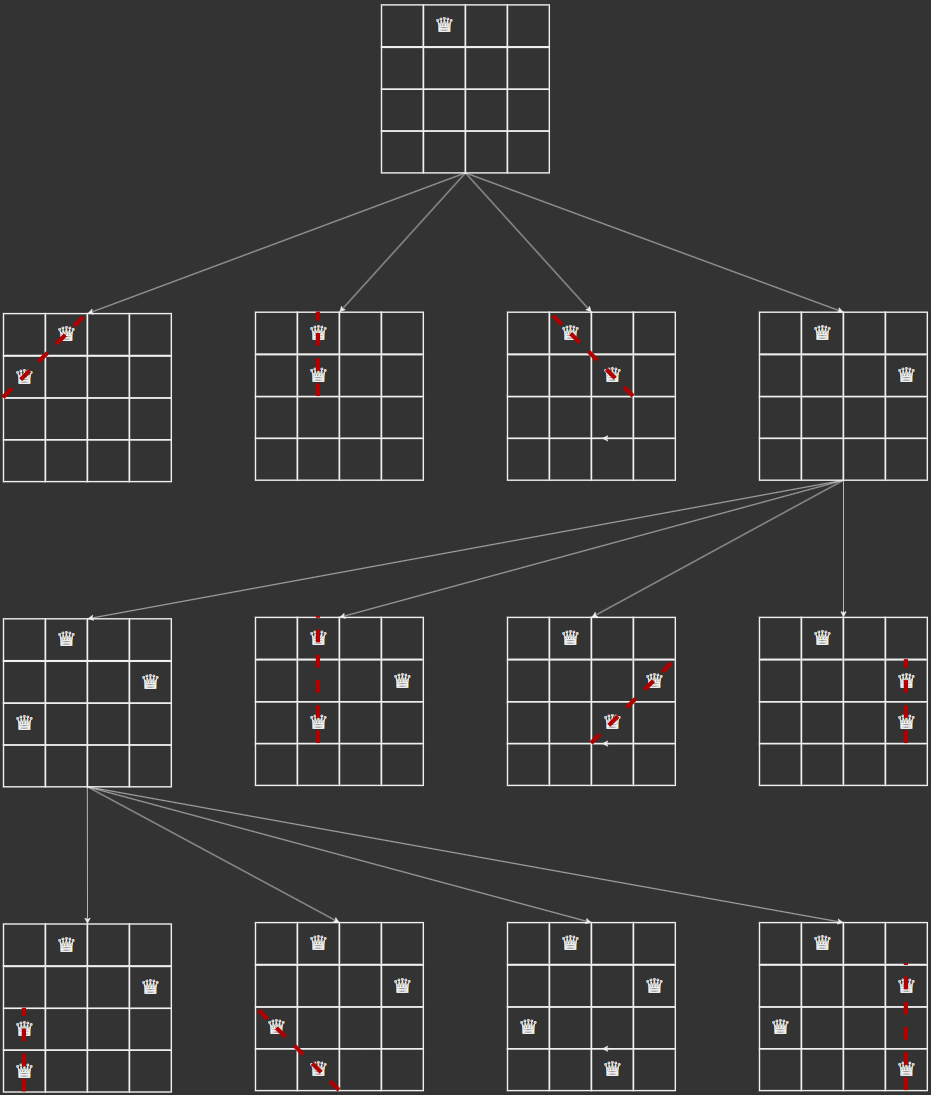
n皇后的约束条件有三个:皇后不能在同一行、同一列和同一条对角线上。
我们采用逐行放置的方式,从第一行开始,每行放置一个皇后,直到最后一行。因为每一行只能存在一个皇后,因此逐行放置起到了剪枝的作用。
接下来需要根据列和对角线进行剪枝。由于棋盘是
n*n大小,对于列来说,可以用长度为n的boolean数组cols记录每一列是否有皇后。对于对角线来说,我们将其分为主对角线(从左上到右下)和次对角线(从右上到左下)。对于棋盘每一格的索引
(row, col),可以发现在主对角线上的索引row - col都为定值,在次对角线上的索引row + col都为定值。因此我们可以用row1 - col1 == row2 - col2来判断两个皇后在不在同一条主对角线上,同理对于次对角线也可以如此处理。在主对角线上,
row - col最小值在左下角,为-n + 1,最大值在右上角,为n - 1,因此其取值范围为[-n+1, n-1]。同理得到次对角线的取值范围为[0, 2n-2]。我们分别用diags1和diags2两个数组来记录对角线上是否有皇后,数组的长度都为2n - 1。代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57class Solution {
List<List<List<String>>> result = new ArrayList<>();
public List<List<List<String>>> solveNQueens(int n) {
List<List<String>> state = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<String> row = new ArrayList<>();
for (int j = 0; j < n; j++) row.add(".");
state.add(row);
}
// 列、主对角线、副对角线是否有皇后
boolean[] cols = new boolean[n];
boolean[] diags1 = new boolean[2 * n - 1];
boolean[] diags2 = new boolean[2 * n - 1];
backtrack(0, n, state, cols, diags1, diags2);
return result;
}
private void backtrack(int row,
int n,
List<List<String>> state,
boolean[] cols,
boolean[] diags1,
boolean[] diags2) {
// 逐行搜索,当放置完所有行时记录解
if (row == n) {
List<List<String>> copyState = new ArrayList<>();
for (List<String> rowState : state) {
copyState.add(new ArrayList<>(rowState));
}
result.add(copyState);
return;
}
// 计算所有列
for (int col = 0; col < n; col++) {
// 主对角线
int diag1 = row - col + n - 1;
// 副对角线
int diag2 = row + col;
// 剪枝,该格所在列、主对角线、副对角线不能存在其他皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 放置皇后
state.get(row).set(col, "Q");
diags2[diag2] = true;
diags1[diag1] = diags2[diag2];
cols[col] = diags1[diag1];
// 递归搜索下一行
backtrack(row + 1, n, state, cols, diags1, diags2);
// 撤销皇后
state.get(row).set(col, ".");
diags2[diag2] = false;
diags1[diag1] = diags2[diag2];
cols[col] = diags1[diag1];
}
}
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59class Solution {
private val result = mutableListOf<MutableList<MutableList<String>>>()
fun solveNQueens(n: Int): List<List<List<String>>> {
val state = mutableListOf<MutableList<String>>()
for (i in 0..<n) {
val row = mutableListOf<String>()
for (j in 0..<n) row.add(".")
state.add(row)
}
// 列、主对角线、副对角线是否有皇后
val cols = BooleanArray(n)
val diags1 = BooleanArray(2 * n - 1)
val diags2 = BooleanArray(2 * n - 1)
backtrack(0, n, state, cols, diags1, diags2)
return result
}
private fun backtrack(
row: Int,
n: Int,
state: MutableList<MutableList<String>>,
cols: BooleanArray,
diags1: BooleanArray,
diags2: BooleanArray
) {
// 逐行搜索,当放置完所有行时记录解
if (row == n) {
val copyState = mutableListOf<MutableList<String>>()
for (cRow in state) {
copyState.add(cRow.toMutableList())
}
result.add(copyState)
return
}
// 计算所有列
for (col in 0..<n) {
// 主对角线
val diag1 = row - col + n - 1
// 副对角线
val diag2 = row + col
// 剪枝,该格所在列、主对角线、副对角线不能存在其他皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 放置皇后
state[row][col] = "Q"
diags2[diag2] = true
diags1[diag1] = diags2[diag2]
cols[col] = diags1[diag1]
// 递归搜索下一行
backtrack(row + 1, n, state, cols, diags1, diags2)
// 撤销皇后
state[row][col] = "."
diags2[diag2] = false
diags1[diag1] = diags2[diag2]
cols[col] = diags1[diag1]
}
}
}
}
注:本笔记参考krahets的hello-algo,仅用于本人记录。